ㅇ 정렬이란?
데이터를 정해진 기준에 따라 배치해 의미 있는 구조로 재설정하는 것이다. 즉, 내림차 순이나 오름차 순으로 다시 배치하는 것이다.
ㅇ 정렬의 종류
① 버블 정렬(Bubble Sort) : 데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식
② 선택 정렬(Selection Sort) : 대상에서 가장 크거나 작은 데이터를 찾아가 선택을 반복하면서 정렬하는 방식
③ 삽입 정렬(Insertion Sort) : 대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식
④ 퀵 정렬(Quick Sort) : pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식
⑤ 병합 정렬(Merge Sort) : 이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식
⑥ 기수 정렬(Radix Sort) : 데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식
정렬의 종류는 다음과 같다. 그렇다면 오늘 알아볼 버블 정렬은 무엇일까.
ㅇ 버블 정렬(Bubble Sort)
두 인접한 데이터의 크기를 비교해 정렬하는 방법이다. 시간복잡도는 O(n²)이지만, 간단하게 구현할 수 있어 자주 사용한다.
이 정렬의 이름이 버블정렬인 이유는 데이터의 이동이 거품이 수면으로 올라오는 듯한 모습을 보이기 때문에 지어진 이름이라고 한다.
왜 시간복잡도가 O(n²)인지 살펴보자.
ㅇ 버블정렬의 이해
버블정렬의 과정은 다음과 같다.
① 앞에서부터 인접한 데이터 값을 비교한다.
② 현재 데이터와 다음 데이터를 비교한다.
③ 만약 다음 데이터가 더 작다면 위치를 바꾸고 아니라면 그대로 둔다.
④ 다음 데이터로 이동하여 값을 비교한다.
이 과정이 반복적으로 있는 것이다.
5 4 1 3 2 라는 배열을 초기 상태를 두고 그림으로 표현하면 다음과 같다.
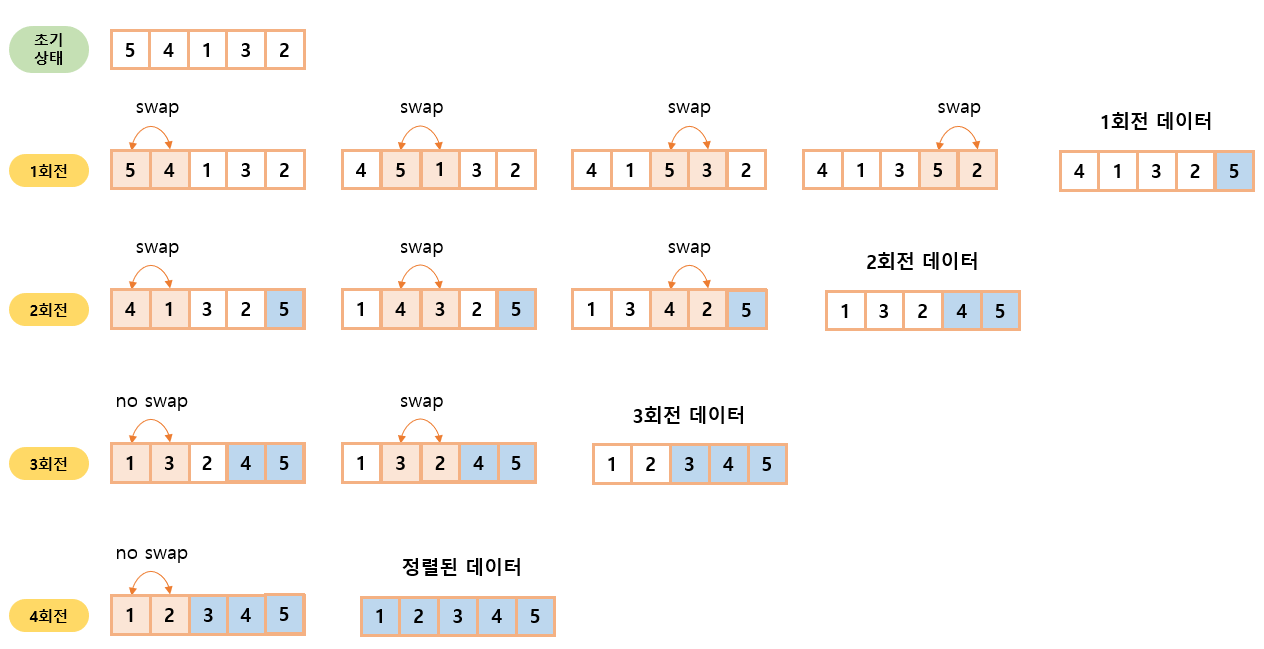
각 회전이 지속될 수록 뒤에서부터 정렬된 모습을 확인할 수 있다.
정리하면,
회전은 배열크기 - 1 번 수행하고,
비교연산은 배열크기 - 라운드 횟수 번 수행한다.
즉, n-1번씩 비교하는 것을 n번 반복하는 것이기 때문에 총 시간 복잡도는 O(N²)이다.
ㅇ 버블정렬의 코드
class Main {
public static int[] arr = new int[5];
public static void main(String[] args) {
arr = new int[]{5, 4, 1, 3, 2};
bubbleSort(arr);
for(int i=0; i<arr.length; i++) {
System.out.print(arr[i] + " " );
}
}
static void bubbleSort(int[] arr) {
int temp = 0;
for(int i = 0; i < arr.length - 1; i++) {
for(int j= 1 ; j < arr.length-i; j++) {
if(arr[j]<arr[j-1]) {
temp = arr[j-1];
arr[j-1] = arr[j];
arr[j] = temp;
}
}
}
}
}
먼저 arr을 5 4 1 3 2라는 정렬되지 않은 배열로 초기화한 후, bubbleSort(arr)을 수행한다.
bubbleSort에서는 arr의 index를 0부터 돌아가면서 인접한 배열과 비교를 한다.
비교 연산을 사용할 때는 temp라는 변수를 따로 할당하여 배열의 위치를 변경하였다.
ㅇ 버블정렬 정리
버블정렬은 간단한 만큼 빠른 속도로 수행되지 않아 효율적으로 알고리즘을 짜야하는 경우에는 거의 사용하지 않습니다.
또한, 정렬하는데 있어 다른 배열을 사용하지 않아 제자리 정렬 알고리즘이라고도 합니다.
이해가 안되신다면 손으로 하나하나 그려가면서 이해하는 것을 추천드립니다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] JAVA 정렬 알고리즘 - 삽입정렬(Insertion Sort) (0) | 2023.02.20 |
|---|---|
| [Algorithm] JAVA 정렬 알고리즘 - 선택정렬(Selection Sort) (0) | 2023.02.16 |
| [Algorithm] JAVA 소수판별 - 에라토스테네스의 체 (2) | 2023.02.06 |
| [Algorithm] 알고리즘 선택의 기준, 시간복잡도 (Big-O 표기법) (2) | 2023.02.06 |
