ㅇ 정렬이란?
데이터를 정해진 기준에 따라 배치해 의미 있는 구조로 재설정하는 것이다. 즉, 내림차 순이나 오름차 순으로 다시 배치하는 것이다.
ㅇ 정렬의 종류
① 버블 정렬(Bubble Sort) : 데이터의 인접 요소끼리 비교하고, swap 연산을 수행하며 정렬하는 방식
② 선택 정렬(Selection Sort) : 대상에서 가장 크거나 작은 데이터를 찾아가 선택을 반복하면서 정렬하는 방식
③ 삽입 정렬(Insertion Sort) : 대상을 선택해 정렬된 영역에서 선택 데이터의 적절한 위치를 찾아 삽입하면서 정렬하는 방식
④ 퀵 정렬(Quick Sort) : pivot 값을 선정해 해당 값을 기준으로 정렬하는 방식
⑤ 병합 정렬(Merge Sort) : 이미 정렬된 부분 집합들을 효율적으로 병합해 전체를 정렬하는 방식
⑥ 기수 정렬(Radix Sort) : 데이터의 자릿수를 바탕으로 비교해 데이터를 정렬하는 방식
ㅇ 선택 정렬 (Selection Sort)
대상 데이터에서 최솟(최댓)값을 찾아 "선택"하여 "선택된 최솟(최댓)값"을 차례대로 바꿔가면서 정렬하는 방법이다.
구현이 복잡하고, 시간 복잡도도 O(n²)으로 효율적이지 않아 코딩테스트에서는 많이 사용하지 않는다.
ㅇ 선택 정렬의 이해
선택 정렬의 과정은 다음과 같다.
① 남은 데이터에서 최솟(최대)값을 찾는다.
② 남은 데이터에서 가장 앞에 있는 데이터와 선택된 데이터를 바꾼다(swap).
③ 가장 앞에 있는 데이터의 위치를 변경해 (index++) 남은 정렬 부분의 범위를 축소한다.
④ 전체 데이터 크기만큼 index가 커질 때까지, 즉 남은 정렬 부분이 없을 때까지 반복한다.
이 과정이 반복적으로 있는 것이다.
5 4 1 3 2 라는 배열을 초기 상태를 두고 그림으로 표현하면 다음과 같다.
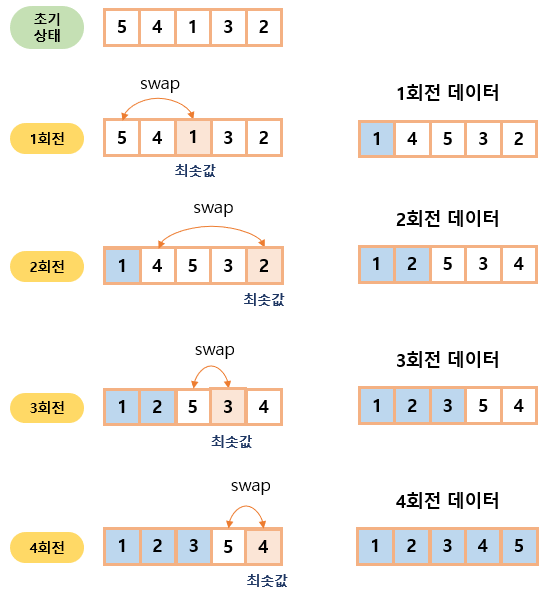
최솟값을 찾아 앞에서부터 나열하기 때문에 앞에서부터 배열된 모습을 확인할 수 있다.
선택 정렬은 앞 index(0)부터 비교하면서 최솟값을 찾는다.
1회전에는 index가 0(나열할 대상 데이터)이며, 처음 데이터부터 마지막 데이터까지 비교하며 최솟값을 찾는다. 최솟값은 1이므로 index[0] 데이터와 자리를 바꾼다.
2회전에는 index가 1(나열할 대상 데이터)이며, index[1] 데이터부터 마지막 데이터까지 비교하며 최솟값을 찾는다. 최솟값은 2이므로 index[1] 데이터와 자리를 바꾼다.
3회전에는 index가 2(나열할 대상 데이터)이며, index[2] 데이터부터 마지막 데이터까지 비교하며 최솟값을 찾는다. 최솟값은 3이므로 index[2] 데이터와 자리를 바꾼다.
4회전에는 index가 3(나열할 대상 데이터)이며, index[3] 데이터부터 마지막 데이터까지 비교하며 최솟값을 찾는다. 최솟값은 4이므로 index[3] 데이터와 자리를 바꾼다.
선택정렬의 시간 복잡도를 빅오(Big-O) 기법을 적용하면 총 두 가지의 계산을 한다.
첫번째는 비교 연산의 횟수를 계산하는 것이다.
1회전부터 마지막 회전까지 n-1번, n-2번, ... , 1번의 횟수로 최솟값을 찾는다. 즉, (n-1) + (n-2) + ... + 1 = n(n-1)/2번이다.
두 번째는 교환 연산의 횟수를 계산하는 것이다.
교환 횟수는 데이터들의 위치를 바꾸는 경우의 수에 비례하여 교환 연산의 횟수는 n-1번이다.
따라서 선택 정렬의 시간 복잡도는 비교 연산의 횟수와 교환 연산의 횟수를 더한 것으로 O(n²)이다.
데이터의 크기가 작으면 알고리즘이 간단하여 사용하기 수월하지만, 데이터의 크기가 커질 수록 오래 걸리기 때문에 다른 알고리즘을 사용하는 것이 좋다.
ㅇ 선택 정렬 자바 코드
class Main {
public static int[] arr = new int[5];
public static void main(String[] args) {
arr = new int[]{5, 4, 1, 3, 2};
selectionSort(arr);
for(int i=0; i<arr.length; i++) {
System.out.print(arr[i] + " " );
}
}
static void selectionSort(int[] arr) {
for (int i=0; i<arr.length-1; i++) {
int minIdx = i;
for (int j=i+1; j<arr.length; j++) {
if (arr[j] < arr[minIdx]) {
minIdx = j;
}
}
int temp = arr[i];
arr[i] = arr[minIdx];
arr[minIdx] = temp;
}
}
}
먼저 arr을 5 4 1 3 2라는 정렬되지 않은 배열로 초기화한 후, selectionSort(arr)을 수행한다.
selectionSort에서는 arr의 index를 0부터 데이터의 크기-1까지 회전하며, 최솟값을 가지는 인덱스를 i로 설정한다.
각 회전에서는 i+1부터 마지막 데이터까지 비교하며 최솟값을 가지는 인덱스를 찾는다.
그 후, 현재 데이터와 최솟값을 가지는 데이터를 교환한다.
ㅇ 선택 정렬 정리
> 메모리 소모가 적으며, 뒤의 index로 갈수록 최솟값을 찾는 범위가 점점 줄어든다.
> 안정성을 만족하지 않는다.
이 특징은 선택 알고리즘을 찾아보면서 알게 되었는데 만약 값이 같은 데이터가 있다면 그 데이터가 어디있느냐에 따라 결과값이 변경될 수 있다는 것이다.
만약 [(연필, 100) , (펜, 50) , (지우개, 50) , (가위, 150)] 가 있다면 가격 순대로 나열하고, 가격이 같다면 가나다 순으로 정렬한다고 해보자.
가격순으로 정렬을 하면
round1 : [(펜, 50) , (연필, 100) , (지우개, 50) , (가위, 150)]
round2 : [(펜, 50) , (지우개, 50) , (연필, 100) , (가위, 150)]
round3 : [(펜, 50) , (지우개, 50) , (연필, 100) , (가위, 150)]
가나다 순으로 정렬하면 지우개가 더 앞에 있어야 한다.
즉, 지우개가 펜보다 앞에 위치하고 있으면 주어진 조건을 만족하며 배열할 수 있지만
지우개가 펜보다 뒤에 위치하고 있다면, 주어진 조건을 만족시키지 않는다.
이 특징이 안정성을 만족하지 않는다고 한다.
'Algorithm' 카테고리의 다른 글
| [Algorithm] JAVA 정렬 알고리즘 - 삽입정렬(Insertion Sort) (0) | 2023.02.20 |
|---|---|
| [Algorithm] JAVA 정렬 알고리즘 - 버블정렬(Bubble Sort) (0) | 2023.02.08 |
| [Algorithm] JAVA 소수판별 - 에라토스테네스의 체 (2) | 2023.02.06 |
| [Algorithm] 알고리즘 선택의 기준, 시간복잡도 (Big-O 표기법) (2) | 2023.02.06 |
